2D Cellular Automata: Three-state Majority Rule

In the previous post I've shown the evolution of elementary cellular automata (CA) for different rules. Now we'll go to the next step and check out a 2D cellular automata model. Just as in 1D CA, the value of a cell in a 2D CA model is dictated by its neighbors. However, for 1D CA a cell only has two neighbors whereas for a 2D CA a cell can have either four or eight neighbors depending on the neighborhood type we are considering. 

So what are these neighborhood types? There are two:

Neighborhood Types

1. Moore neighborhood

The Moore neighborhood consists of the eight cells surrounding a central cell in a 2D lattice. The figure below shows an illustration of the Moore neighborhood. 

2. Von Neumann neighborhood

The Von Neumann neighborhood is comprised of the four cells orthogonal to a central cell as shown in the image below.

Figure 1. The blue cells indicate the neighbors of the central cell (orange cell)
for the Moore neighborhood (left) and the Von Neumann neighborhood (right) 

There are several 2D cellular automata models that are currently used to model systems, such as the simple binary majority rule, Conway's Game of Life, the Schelling model, Turing patterns, and the Sandpile model. 

Majority Rule

For this post we'll be dealing with the simplest of these: the majority rule. As the name of the model suggests, the value of a cell is updated depending on which state is most dominant among its neighbors. Here, we model a three-state system with a Moore neighborhood starting with an initially random distribution of states and letting the system evolve in time while taking note of the following rules:

1. When there exists a dominant state $S_{maj}$ among the three states $S = {0, 1, 2}$ in the neighborhood, the value of the central cell is updated to $S_{maj}$.

2. In case there is no clear dominant state (i.e. in case of a tie in the frequency of some states) in the neighborhood then the value of the central cell is unchanged.

Shown below are snapshots of the 2D lattice over several iterations for different lattice sizes.

Evolution of an 8x8 lattice for three-state majority rule

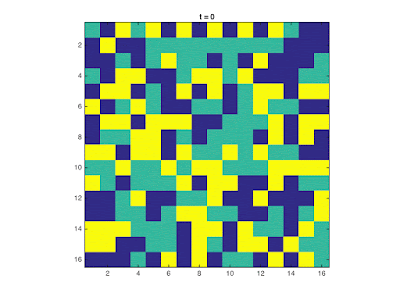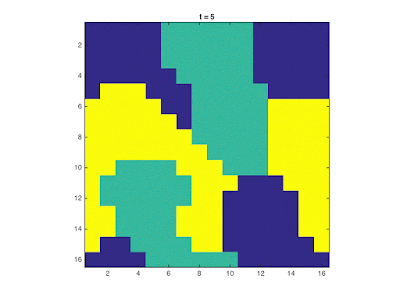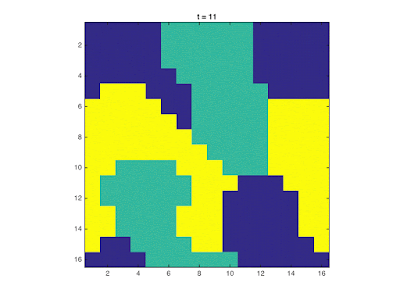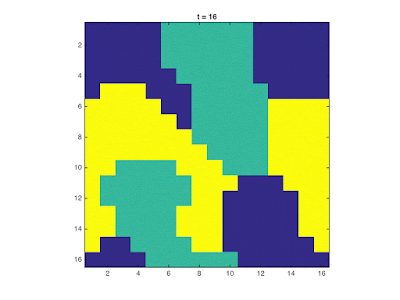Evolution of a 16x16 lattice for three-state majority rule

Evolution of a 32x32 lattice for three-state majority rule

Evolution of a 64x64 lattice for three-state majority rule

It can be observed, especially for $N>8$,  that as the system evolves it reaches a steady state. From the considered systems, it is possible to achieve a "unanimous" state in which all cells have equal values or a steady state in which no clear majority exists in the Moore neighborhood of all cells so the system no longer evolves and stays in this state. 

Collaborators:

Mary Angelie M. Alagao

Maria Eloisa M. Ventura